GLSL : animation de déformation de cibles

L'animation de déformation de cibles (Morph target animation) est une technique qui permet de déformer un modèle en utilisant de multiples versions déformées de ce même modèle. Cette technique est par exemple utilisée dans l'animation des personnages. Les versions déformées sont les cibles de déformation (aussi appelées formes mixées [blend shapes]). La déformation d'une cible vers une autre est effectuée à l'aide d'une interpolation linéaire entre les positions des sommets.

Voici une technique simple de déformation par cibles qui stocke les positions des sommets des cibles dans le modèle original en utilisant les tableaux d'attributs de sommets (glVertexAttribPointer en OpenGL). Toutes les cibles de déformation doivent avoir le même nombre de sommets. Tout le travail d'animation est effectué dans le vertex shader.

Voici le vertex shader en GLSL en action : une déformation entre un torus et un cylindre.

Les démonstrations (en Lua et GLSL) sont codées avec GLSL Hacker (Windows, OS X et Linux) et sont disponibles dans le dossier moon3d/gl-320-mesh-morphing/, dans la dernière version d'exemples. Il est recommandé de récupérer la dernière version de développement (pour GLSL Hacker et pour les codes d'exemples).

Comme toujours, les shaders GLSL suivants peuvent être utilisés, après seulement quelques modifications (le nom des entrées du shader), dans n'importe quelle application OpenGL supportant ce genre de fonctionnalités.

Dans GLSL Hacker, le sommet a une structure comme suit :

vertex 
{ 
  vec4 Position; 
  vec4 Color; 
  vec4 Normal; 
  vec4 Tangent; 
  vec4 TexCoord0; 
  vec4 TexCoord1; 
}

Dans les démonstrations, nous allons allouer de nouveaux attributs de sommets pour conserver la position des cibles de déformation (dans le script Lua, l'allocation est effectuée avec gh_mesh.alloc_user_vertex_attribs()). Pour garder les positions des deux cibles de déformation, nous avons besoin de deux nouveaux attributs de sommet : attrib0 etattrib1. Le sommet possède maintenant cette structure :

vertex 
{ 
  vec4 Position; 
  vec4 Color; 
  vec4 Normal; 
  vec4 Tangent; 
  vec4 TexCoord0; 
  vec4 TexCoord1; 
  vec4 Attrib0; 
  vec4 Attrib1; 
}

Dans les vertex shaders de cet article, Attrib0 et Attrib1 sont gxl3d_Attrib0 et gxl3d_Attrib1.

La première démonstration montre la transformation entre un tore et un cylindre. Dans le vertex shader suivant, gxl3d_Position contient les positions du tore, gxl3d_Attrib0 contient les couleurs du sommet et gxl3d_Attrib1 les positions du cylindre (les tableaux d'attributs de sommets ont été initialisés dans le script Lua avec gh_mesh.set_user_vertex_attrib()). La variable uniforme appelée « time » (temps) varie entre 0.0 et 1.0. Le vertex shader utilise une interpolation linéaire (lerp) :

#version 150 
in vec4 gxl3d_Position; 
in vec4 gxl3d_Attrib0; 
in vec4 gxl3d_Attrib1; 
out vec4 Vertex_Color; 
uniform mat4 gxl3d_ModelViewProjectionMatrix; 
uniform float time; 
void main() 
{ 
  vec4 P; 
  P = gxl3d_Position + (gxl3d_Attrib1 - gxl3d_Position) * time; 
  gl_Position = gxl3d_ModelViewProjectionMatrix * P; 
  Vertex_Color = gxl3d_Attrib0; 
}

L'interpolation linéaire :

P = gxl3d_Position + (gxl3d_Attrib1 - gxl3d_Position) * time;

peut être réécrite avec la fonction intégrée du GLSL : mix().

P = mix(gxl3d_Position, gxl3d_Attrib1, time);

La démonstration est aussi disponible avec une meilleure interpolation basée sur la fonction smoothstep. Le vertex shader suivant montre une interpolation adoucie basée sur la fonction intégrée du GLSL smoothstep() ou basée sur une implémentation directe (la définition SMOOTHSTEP) :

#version 150 
in vec4 gxl3d_Position; 
in vec4 gxl3d_Attrib0; 
in vec4 gxl3d_Attrib1; 
out vec4 Vertex_Color; 
uniform mat4 gxl3d_ModelViewProjectionMatrix; 
uniform float time; 
#define SMOOTHSTEP(x) ((x) * (x) * (3 - 2 * (x))) 
void main() 
{ 
  //float alpha = SMOOTHSTEP(time); 
  float alpha = smoothstep(0.0, 1.0, time); 
  vec4 P = (gxl3d_Position * alpha) + (gxl3d_Attrib1 * (1 - alpha)); 
  gl_Position = gxl3d_ModelViewProjectionMatrix * P; 
  Vertex_Color = gxl3d_Attrib0; 
}

Ou en utilisant la fonction mix() :

P = mix(gxl3d_Position, gxl3d_Attrib1, smoothstep(.0,1.,time));

Une autre méthode d'interpolation intéressante est l'interpolation linéaire sphérique (ou slerp) :

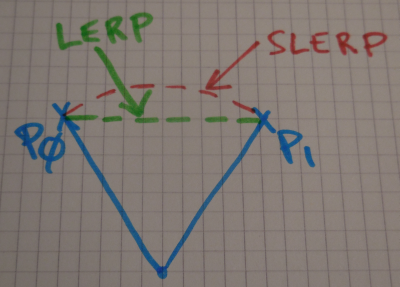
Voici le vertex shader avec l'interpolation SLERP :

#version 150 
in vec4 gxl3d_Position; 
in vec4 gxl3d_Attrib0; 
in vec4 gxl3d_Attrib1; 
out vec4 Vertex_Color; 
uniform mat4 gxl3d_ModelViewProjectionMatrix; 
uniform float time; 

vec4 Slerp(vec4 p0, vec4 p1, float t) 
{ 
  float dotp = dot(normalize(p0), normalize(p1)); 
  if ((dotp > 0.9999) || (dotp<-0.9999)) 
  { 
    if (t<=0.5) 
      return p0; 
    return p1; 
  } 
  float theta = acos(dotp * 3.14159/180.0); 
  vec4 P = ((p0*sin((1-t)*theta) + p1*sin(t*theta)) / sin(theta)); 
  P.w = 1; 
  return P; 
} 

void main() 
{ 
  vec4 P = Slerp(gxl3d_Position, gxl3d_Attrib1, time); 
  gl_Position = gxl3d_ModelViewProjectionMatrix * P; 
  Vertex_Color = gxl3d_Attrib0; 
}

Le code provenant de l'archive de codes d'exemples inclut aussi une démonstration qui montre comment utiliser deux cibles de déformation (un tore et un cylindre) pour déformer une sphère. Rien de nouveau ici, simplement la méthode pour gérer deux cibles de déformation. Dans le vertex shader suivant, gxl3d_Position contient les positions de la sphère, gxl3d_Attrib0 contient les couleurs des sommets, gxl3d_Attrib1 les positions de la première cible de déformation (le tore) et gxl3d_Attrib2 contient les positions de la seconde cible de déformation (le cylindre). La variable uniforme time varie entre 0.0 et 2.0.

#version 150 
in vec4 gxl3d_Position; 
in vec4 gxl3d_Attrib0; 
in vec4 gxl3d_Attrib1; 
in vec4 gxl3d_Attrib2; 
out vec4 Vertex_Color; 
uniform mat4 gxl3d_ModelViewProjectionMatrix; 
uniform float time; 
void main() 
{ 
  vec4 P; 
  
  if (time < 1.0) 
    P = gxl3d_Position + (gxl3d_Attrib1 - gxl3d_Position) * time; 
  else 
    P = gxl3d_Attrib1 + (gxl3d_Attrib2 - gxl3d_Attrib1) * (time -1.0); 
  
  gl_Position = gxl3d_ModelViewProjectionMatrix * P; 
  Vertex_Color = gxl3d_Attrib0; 
}

• Animation avec cibles de déformation
• Animation avec des formes mixées
• Rendu de face en GLSL

Cet article est une traduction autorisée de l'article paru sur Geeks3D.com.

Merci à Winjerome pour sa relecture attentive et milkoseck pour sa relecture orthographique.